A time model for PET reference-region data using a GLM implementation of SRTM
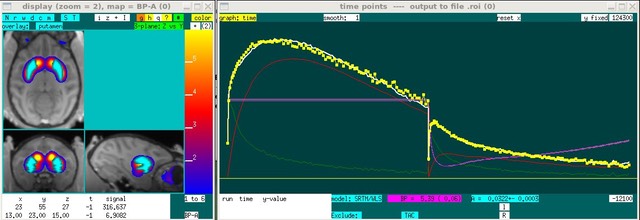
Reference tissue models assume that there exists a reference region, devoid of the receptors of interest, that can be used a surrogate for the plasma concentration of PET ligand in order to avoid arterial blood sampling. The solution to the three-compartment model (plasma, free, & bound ligands) with a reference region, written in terms of the total (free + bound) tissue concentration (CT) , the reference region tissue concentration (CR), and the free concentration (CF) is (e.g., Cunningham 1991):
![]()
For PET tracers with rapid equilibrium between free and bound compartments, the total tissue concentration is simply a scaled version of the free concentration, which produces the operational equation for the simplified reference tissue model (SRTM, Lammertsma 1996):
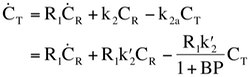 [1]
[1]
Because this equation is linear in parameters, it can be solved by standard methods using the generalized linear model. To convert to tissue concentrations rather than derivatives (and also regularize the equation), an integral form generally is used:
![]() [2]
[2]
This equation now can be solved by GLM for 3 parameters: R1, k2, & k2a, with the binding potential (BP) equal to BP = k2/k2a - 1.
Fixing k'2 as a global constant
The parameter k'2, the washout rate for the reference region, is really a global constant that should not be fit for every voxel. From Eq. 1, it's clear that this value will be biased toward zero in regions without specific binding in order to reduce noise from the last two terms. This bias on k'2 then can effect other parameters, so a good strategy for mapping is to determine k'2 using a 3-parameter fit and then fix it as a global constant and fit only 2 parameters per voxel:
![]() [3]
[3]
Dynamic binding potentials
A binding potential, by definition, can only be defined at equilibrium for a physiological steady state. This can be a problem for challenge data, because this steady-state requirement is not suitable to describe the biology, so it is often better to turn k2a into a dynamic quantity under such circumstances (Alpert 2003). For ligands with a low single-pass extraction fraction (flow doesn't change k2 or R1 very much), this strategy essentially turns BP into a dynamic quantity. However, it's important to remember that while this strategy enables kinetic modeling of challenge data, a "dynamic binding potential" is only an approximation of real changes in receptor availability in the specific binding compartment, because that compartment cannot be isolated from the free & non-specifically bound compartment within SRTM. If k2a is parameterized as a gamma function, for instance, then Eq. 3 is modified as
![]()
Whether or not one converts the net k2a term into a BP-like quantity depends upon the application. This step might be warranted for applications that seek to determine occupancies within a classical competition model. However, the k2a terms are the parameters directly determined by least squares.